语法

1
2
3
4
5
6
7
8
9
string line;     
getline(cin, line); //读一行     
if(line.back() != ')') line += " (+0)";      
int h1, m1, s1, h2, m2, s2, day;     
sscanf(line.c_str(), "%d:%d:%d %d:%d:%d (+%d)", &h1, &m1, &s1, &h2, &m2, &s2, &day);      
int S = h1*3600 + m1*60 + s1; //起飞时间：转为秒     
int E = h2*3600 + m2*60 + s2; //到达时间：转为秒     
int ans = E - S + day*24*3600; //返回秒 
printf("%02d:%02d:%02d\n",ans/3600,ans/60%60,ans%60); //时:分:秒

优先unordered_map,要求顺序的时候用map(自动排序)

二分

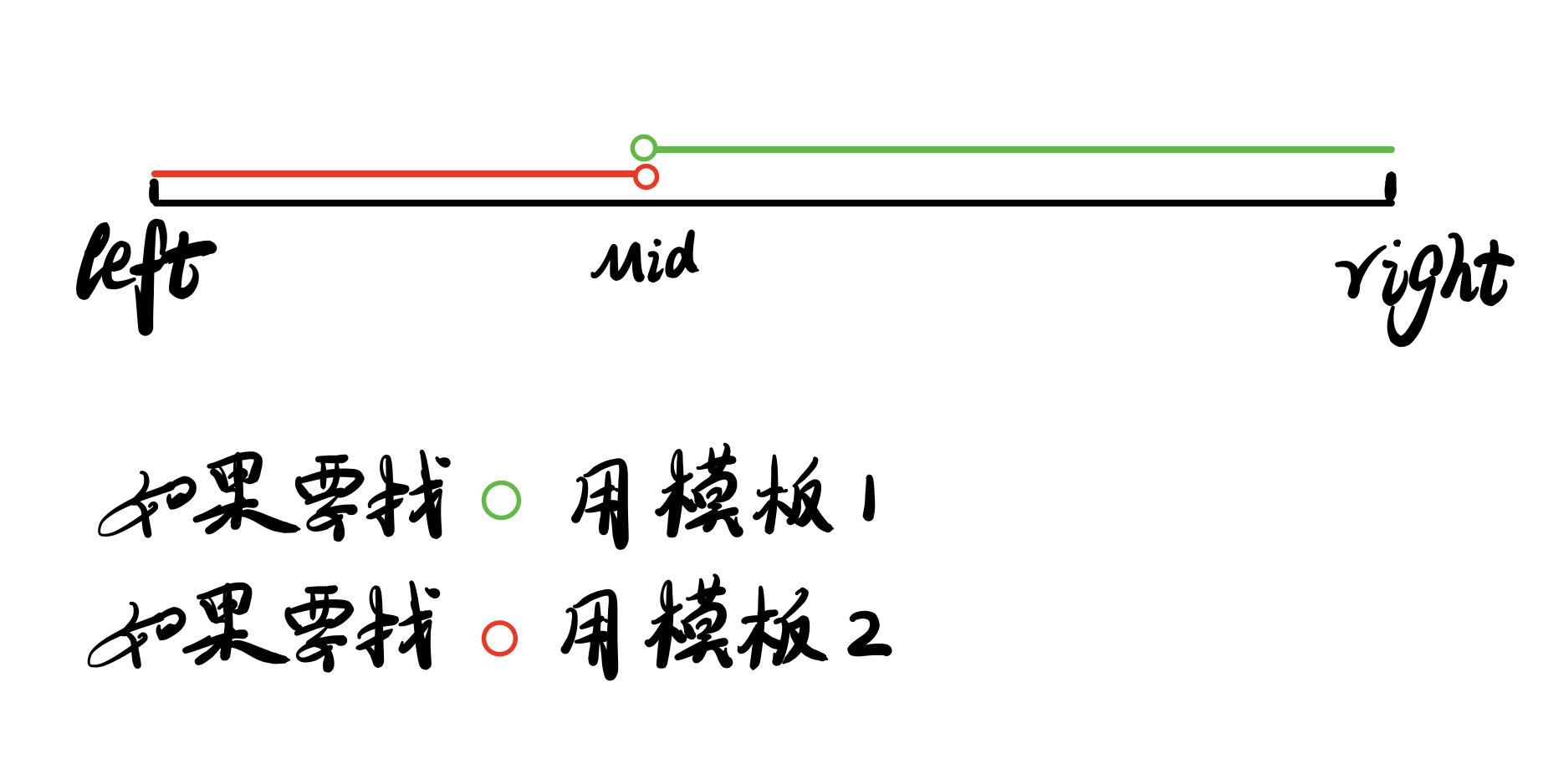
if的判断条件是让mid落在满足你想要结果的区间内

1.循环必须是l < r
2.if判断条件看是不是不满足条件， 然后修改上下界
3.若if else后是r = mid - 1，则前面mid 语句要加1
4.出循环一定是l == r，所以l和r用哪个都可以

img4

二分只有下面两种情况
1：找大于等于给定数的第一个位置 （满足某个条件的第一个数）
2：找小于等于给定数的最后一个数 （满足某个条件的最后一个数）

l r r l 1 lr1lr1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
//查找左边界 SearchLeft 简写SL
// 能二分的题一定是满足某种性质，分成左右两部分
// if的判断条件是让mid落在满足你想要结果的区间内

// 找满足某个条件的第一个数  即右半段
int SL(int l, int r) {
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid)) 
            r = mid; 
        else 
            l = mid + 1; 
    }   
    return l;
}

// 找满足某个条件的最后一个数  即左半段
//查找右边界 SearchRight 简写SR 
int SR(int l, int r) {
    while (l < r) {                   
        int mid = l + r + 1 >> 1; //需要+1 防止死循环
        if (check(mid)) 
            l = mid;
        else 
            r = mid - 1; 
    }
    return r; 
}	

//浮点数
double bsearch_3(double l, double r){
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps){
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

进制转换

十进制转R进制 如果R大于10，可以定义一个转换数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//十进制转十六进制 短除法
char h[17] = {'0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};//十六进制

do{  //不用while循环,处理n == 0的情况
    a[num ++] = n % 16;
    n /= 16;
}while(n != 0);
for(int i = num - 1; i >= 0; i --) cout << h[a[i]];

//十进制转任意进制
string res;
do{
    int y = x % b;
    if (y <= 9)
        res += y + '0';
    else
        res += y - 10 + 'A';
    x /= b;
}while(x != 0);

R进制转十进制 秦九韶算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//十六进制转十进制  跳过前两位
//转化为小写

int res = 0, sgn = 1;
if (str[0] != '-'){
    for (int i = 2; str[i]; i ++ )
        if (isdigit(str[i])) 
            res = res * 16 + str[i] - '0';
        else 
            res = res * 16 + tolower(str[i]) - 'a' + 10;
}
else{
    sgn = -1;
    for (int i = 3; str[i]; i ++ )
        if (isdigit(str[i])) 
            res = res * 16 + str[i] - '0';
    else 
        res = res * 16 + tolower(str[i]) - 'a' + 10;
}
cout << sgn * res << endl;

//2022的九进制转十进制
string s = "2022";
int res = 0;
for(int i = 0; i < s.size(); i++)
	res = res * 9 + s[i] - '0';

日期模板

求从2001年1月1日到2021年12月31日中 有多少个完全日期

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 5, mod = 1e9 + 7;
struct Time
{
    int y, m, d;
};
int res, day[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
void add(Time &a)
{
    a.d++;
    int x = day[a.m];
    if(((a.y % 4 == 0 && a.y % 100 != 0) || a.y % 400 == 0) && a.m == 2) x++; //特判闰年的2月份
    if(a.d > x) a.m++, a.d = 1;
    if(a.m > 12) a.y++, a.m = 1;
}
bool check(Time a)
{
    int s[] = {a.y, a.m, a.d}, y = 0;
    for(int i = 0; i < 3; i++)
    {
        int x = s[i];
        while(x)
        {
            y += x % 10;
            x /= 10;
        }
    }
    int z = sqrt(y);
    return z * z == y;
}
int main()
{
    Time a = {2001, 1, 1}, b = {2021, 12, 31};
    while(a.y != b.y || a.m != b.m || a.d != b.d)
    {
        if(check(a)) res++;
        add(a);
    }
    cout << res;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
int year(int n){
	if((n%4==0&&n%100!=0) || (n%400==0)){
		return 29;
	}
	else{
		return 28;
	}
}
int quzhen(int n){

    int sum=0;
	while(n){
		int k=n%10;
		sum+=k;
		n=n/10;
	}
	return sum;
}
int check(int n){
	int k=sqrt(n);
	if(k*k==n){
		return 1;
	}
	return 0;
}
int main(){
	int day[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
	int ans=0;
	for(int i=2001;i<=2021;i++){
		for(int j=1;j<=12;j++){
			day[2]=year(i);
			for(int z=1;z<=day[j];z++){
				int a=quzhen(i)+quzhen(j)+quzhen(z);
				cout<<i<<" "<<j<<" "<<z<<" "<<a<<" "<<check(a)<<endl;
				if(check(a)){
					ans++;
				}
			}
		}
	}
	cout<<ans<<endl;
	return 0;
}
//977

素数筛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int primes[N], cnt;     // primes[]存储所有素数
bool st[N];             // st[x]存储x是否被筛掉   后续也可以用来加速某些判断·

void get_primes(int n){
    //提前筛掉 
	st[0] = true;
	st[1] = true;
	
    for (int i = 2; i <= n; i ++ ){
        if (!st[i]) 
			primes[cnt++] = i;
        for (int j = 0; primes[j] <= n / i; j++){
            st[primes[j] * i] = true;//被筛掉的  非素数 
            if (i % primes[j] == 0) 
				break;
        }
    }
}

前缀和与差分

涉及到区间的求交 求并集

原数组就是差分数组的前缀和。我们可以举个例子：

原始数组：9 3 6 2 6 8
差分数组：9 -6 3 -4 4 2

高精度加减法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
//加法
vector<int> add(vector<int>& a, vector<int> &b){
	int t = 0;
	vector <int> c;
    
    //手动模拟进位
	for(int i = 0; i < a.size() || i < b.size(); i++){
		if(i < a.size()) t += a[i];
		if(i < b.size()) t += b[i];
		c.push_back(t % 10);
		t /= 10;
	}
	if(t) 
        c.push_back(1);
	return c;
}

//减法
bool cmp(vector<int> &A , vector<int> &B){
    if(A.size() != B.size()) return A.size() > B.size();

    for(int i = A.size() - 1; i >= 0; i --)
        if(A[i] != B[i]) 
            return A[i] > B[i];

    return true;
}

vector<int> sub(vector<int> &A , vector<int> &B){
    int t = 0;
    vector<int> C;
    
    for(int i = 0; i < A.size(); i++){
        t = A[i] - t;
        if(i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if(t < 0) t = 1;
        else t = 0;
    }
    while(C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

//加法
for(int i = a.length() - 1; i >= 0; i--) va.push_back(a[i] - '0');
for(int i = b.length() - 1; i >= 0; i--) vb.push_back(b[i] - '0');
auto vc = add(va,vb);

//减法
if(cmp(a, b))  vc = sub(a, b);     //正数
else vc = sub(b, a) , cout << '-' ; //负数

//输出
for(int i = vc.size() - 1; i >= 0; i--) printf("%d",vc[i]);

离散化

把离散的数据紧凑化，减少遍历次数

1
2
3
4
5
6
7
8
//一般离散的都是位置（下标）
vector<int> alls;
sort(alls.begin(), alls.end()); 
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去重


//找的话  二分把题设中的数组 投射 到离散化的all里面
int pos = lower_bound(alls.begin(), alls.end(), x) - alls.begin() + 1;

裸LCA

求两个节点的最小公共祖先。如果会写倍增版本的LCA，可以快一个数量级。

1
2
3
4
5
6
7
8
9
10
int LCA (int x, int y){
    while(x != y){
        //两个节点没有相遇，让较下面一点的节点往上爬 
        if (x < y)	//这个时候y在下面 
            y >>= 1;
        else		//这个时候x在下面 
            x >>= 1;
	}
    return x;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int l[N], r[N], p[N], d[N];//左、右、父、深度

//获取各结点的深度
void dfs(int root, int depth){
    if(root == -1) 
        return;
    d[root] = depth;
    dfs(l[root], depth+1);
    dfs(r[root], depth+1);
}

//获取两个结点的最近公共祖先
int getParent(int x1, int x2){
    if(d[x1] < d[x2]) 
        return getParent(x2, x1);//维护x1为较深的那个
    while(d[x1] > d[x2]) 
        x1 = p[x1];//x1往上走， 直到与x2深度相同
    while(x1 != x2) 
        x1 = p[x1], x2 = p[x2]; //同时往上走， 直到两结点相同
    return x1;
}

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i++){
        int left, right;
        cin >> left >> right;
        l[i] = left, r[i] = right;
        if(left != -1) 
            p[left] = i;
        if(right != -1) 
            p[right] = i;
    }
    dfs(1, 1);//从根结点1开始遍历， 获取深度

    int x1, x2;
    while( m -- ){
        cin >> x1 >> x2;
        int parent = getParent(x1, x2);
        cout << d[x1] + d[x2] - 2 * d[parent] << endl;
    }

	return 0;
}

字典树

trie树中 二维数组son存的是节点的下标 第一维就是下标的值 第二维代表着儿子（理解为具体元素）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int son[N][26]; // 存储每个结点的所有儿子结点 
// 在题目中，字符串只包含 26 个小写字母
// 因此每个结点最多只会向外连 26 条边 ( 最多只有 26 个儿子结点 )

int cnt[N]; // count，记录以这个结点结尾的单词有多少个  它在本模板中作为 字符串结束标记
int idx; // 存储当前已经使用到的结点的下标   下标是 0 的结点，既是根节点，又是空结点
char str[N]; // 存储输入的字符串 

void insert(char str[]){
    int p = 0; // 每次都从根结点出发 
    for(int i = 0; str[i]; i++) // c++ 字符串结尾是 \0，可用于遍历整个字符串 
    {
        int u = str[i] - 'a'; // 得到当前字母子结点编号
        if( !son[p][u]) 
            son[p][u] = ++idx; // 如果该子结点不存在，创建子结点 
        p = son[p][u]; // 进入该子结点 
    }
    // 上面的 for 循环结束，则要插入的字符串遍历结束
    // 此时 p 对应的就是最后一个字符所在的结点 
    cnt[p] ++; // 在末尾的结点处增加 结束标记 ( 该字符串出现的次数的累加 ) 
}

//查询过程 与插入略相反

int query(char str[]){
	//......
    
    if( !son[p][u] ) return 0;
    
    //......
    return cnt[p]; // 返回以 p 结尾的单词数量
}

线段树

拓扑排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int cnt = 0;

struct edge{
	int to;
	int next;
} e[N];

void add(int u, int v) {
	cnt++;
    e[cnt].to = v;
	e[cnt].next = h[u];
	h[u] = cnt;
}

//只有点和点相连的关系 
while(m--) {
    int x, y;
    cin >> x >> y;
    add(x,y);
    d[y]++;//入度增加 
}

for(int i = 1;i <= n; ++i)// 将所有入度为0的点加入队列
    if(d[i] == 0) 	
        q.push(i);

//弹弹弹
while(!q.empty()){
    int t = q.front();
    q.pop();
    top[index++] = t;  //输出数组
    for(int i = h[t]; i; i = e[i].next){  //链式前向星
        int j = e[i].to;
        d[j]--;
        if(d[j] == 0)
            q.push(j);
    } 
}

//s点到各点的距离 
for(int i = 1; i <= n; i++)
    cout << top[i] << ' ';

Floyd

1
2
3
4
5
6
7
8
9
10
11
12
13
//边权数组初始化
for(int i = 1; i <= n; i++)
    for(int j = 1; j <= n; j++)
        if(i == j) 
            d[i][j] = 0;
        else 
            d[i][j] = INF;

//三重循环弗洛伊
for(int k = 1; k <= n; k++)
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

数论

容斥原理

求矩形交集等

约数

算数基本定理

img

如果 N = p1^c1 * p2^c2 * … *pk^ck
约数个数： (c1 + 1) * (c2 + 1) * … * (ck + 1)
约数之和： (p1^0 + p1^1 + … + p1^c1) * … * (pk^0 + pk^1 + … + pk^ck

合数一定可以分解成唯一的一组质数的乘积

翡蜀定理

关于ax + by=cax + by=c 有整数解的定理：设a，b是整数且 gcd(a, b) = d，

  • 如果d不能整除c，那么方程ax+by=c没有整数解
  • 如果d能整除c，那么存在无穷多个整数解
  • 不难得知，a与b互质时，也存在无穷多个整数解

模运算

运算的结合律： (a+b) % p = (a%p + b %p) %p

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//试除法分解质因数 
void divide(int x) {
   for (int i = 2; i <= x / i; i ++ ){
       if (x % i == 0) {
           int s = 0;
           while (x % i == 0) {
               x /= i;
               s++;
           }
           cout << i << '^' << s << endl;
       }
   }
    
   //自己没有任何约数  直接输出自己
   if (x > 1) 
       cout << x << '^' << 1 << endl;
}

//试除法求所有约数
vector<int> res;
void get_divisors( int x) {
    for (int i = 1; i <= x / i; i ++ ){
        if (x % i == 0) {
            res.push_back(i);
            if (i != x / i)
            	res.push_back(x / i);
    	}
    }
    sort(res.begin(), res.end());
}

//快速幂 p可以为题中给出的值  也可以为 1e18 等
long long quick_power(int a, int b, int p){
    long long ans = 1 % p;
    while (b) {
        if (b & 1) 
            ans = (long long)ans * a % p;
        a = (long long)a * a % p;
        b >>= 1;
    }
    return ans;
}

归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void merge_sort(int l,int r){
    int mid = (l + r) >> 1;
    
    //往两边递归
    merge_sort(l, mid);
    merge_sort(mid + 1,r);
    
    int i = l,j = mid + 1,k = 0;
    
    //两段比较赋值
    while(i <= mid && j <= r){
        if(a[i] <= a[j]) 
            tmp[k++] = a[i++];
        else{
            //cnt += (mid - i + 1);
            tmp[k++] = a[j++];
        }
    }
    
    //剩余的继续赋值
    while(i <= mid) 
        tmp[k++] = a[i++];
    while(j <= r) 
        tmp[k++] = a[j++];
}

滑动窗口

维护一个单调递增的双向队列。窗口前进条件：①窗口尺寸超出k，删除队头 ②队尾小于当前元素，删除队尾并添加当前元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//求窗口大小为k的区间 其中的最小值
//队列中存入下标
for (int i = 0; i < n; ++i) {

    //注意非空的判断
    //单调递增
    while(!q.empty() && i - k >= q.front())
        q.pop_front(); 

    //队列最后的元素 大于等于 当前元素  （X X 5）4
    while(!q.empty() && a[q.back()] >= a[i])
        q.pop_back();
    q.push_back(i);

    //每次pop和push结束后 就输出
    if(i + 1 >= k)
    	cout << a[q.front()] << ' ' ;//
}

区间贪心

求最大不相交的区间个数

按右端点排序，则直接比较。否则用优先队列维护右端点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

//n个区间，最少选择多少个点，可以保证每个区间至少包含一个选择的点
//翻译：求不相交的区间个数 

int n;
//右端点排序 
struct Range{
    int l, r;
    bool operator< (const Range &W)const {
        return r < W.r;
    }
}range[N];

int main(){
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d%d", &range[i].l, &range[i].r);

    sort(range, range + n); // 排序

    int res = 0, ed = -2e9; // ed表示当前选点
    for (int i = 0; i < n; i ++ )
        if (range[i].l > ed) // 如果覆盖不了这个区间
        {
            res ++ ; // 选点数量增加
            ed = range[i].r; // 更新选点
        }

    printf("%d\n", res);

    return 0;
}

Dijkstra

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
typedef pair<int,int> PII; // 距离  节点
priority_queue<PII, vector<PII>, greater<PII>> q;//小根堆 小到大排序 
     
int n, m, s;
int dist[N];
int h[N], cnt;//链表头结点  结点数字标号
bool st[N];// 存储每个点的最短距离是否已确定

struct edge{
	int to;
	int w;
	int next;
} e[N];// 邻接表存储所有边

void add(int u, int v, int w) {
	cnt++;
    e[cnt].to = v;
	e[cnt].w = w;
	e[cnt].next = h[u];//注意顺序
	h[u] = cnt;        //注意顺序
}
// first存储距离，second存储节点编号
void f() {
    
    dist[s] = 0;
    q.push({0, s});//放入起始点 {距离，结点}
	while(!q.empty()) {
        
        //取出当前距离最小的点
        auto t = q.top();
        q.pop();
        int dis = t.first;
        int ver = t.second;

        //没有被访问过
        if(!st[ver]){
            st[ver] = true;
            
            //按边遍历
            for(int i = h[ver]; i; i = e[i].next) {
                int j = e[i].to;//取出到达点
                if(dist[j] > dis + e[i].w) {
                    dist[j] = dis + e[i].w;
                    q.push({dist[j], j});
                }
            } 
        }
    }
}

//在main函数里 dist初始化为无穷大

SPFA

dijkstra是基于贪心的思想，每次选择最近的点去更新其它点，过后就不再访问。

spfa算法，只要有某个点的距离被更新了，就把它加到队列中，去更新其它点，所有每个点有被重复加入队列的可能。st是一个集合，不是检验队列中的点。用到的时候就加入到集合中，否则就弹出集合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
queue<int> q; //只放点 不放距离

void f() {
    q.push(s);
    st[s] = true; //集合中加入起点

    while(!q.empty()) {

        int t = q.front();
        q.pop();

        st[t] = false;  //弹出

        for(int i = h[t]; i; i = e[i].next) {
            int j = e[i].to;

            if(dist[j] > dist[t] + e[i].w) {
                dist[j] = dist[t] + e[i].w; //先更新好
                
                //如果不在集合中
                if(!st[j]){
                    st[j] = true;
                    q.push(j);
                }
            }
        } 
    }
}

引申：判断是否存在负环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
queue<int> q; //只放点

bool f() {
    
    /*首先距离不需要初始化*/
    /*将所有点入队，可以防止有的点不能走到负环*/
	for(int i = 1; i <= n; i++){
		q.push(i);
		st[i] = true; //每个 点 都有可能是 环的 "起点"
	}

    while(!q.empty()) {

        int t = q.front();
        q.pop();

        st[t] = false;  //弹出

        for(int i = h[t]; i; i = e[i].next) {
            int j = e[i].to;

            if(dist[j] > dist[t] + e[i].w) {
                dist[j] = dist[t] + e[i].w; //先更新好
                
                // 如果某条最短路径上有 n 个点（除了自己），那么加上自己之后一共有 n + 1 个点，
                // 由抽屉原理一定有两个点相同，所以存在环。
                cnt[j] = cnt[t] + 1;
				if(cnt[v] >= n) 
                    return true;
                
                if(!st[j]){
                    st[j] = true;
                    q.push(j);
                }
            }
        } 
    }
    
    return false;
}

并查集

(1)朴素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int p[N]; //存储每个点的祖宗节点

// 返回x的祖宗节点
int find(int x){
    if (p[x] != x) 
    	p[x] = find(p[x]);
    return p[x];
}

// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;

// 合并a和b所在的两个集合：
p[find(a)] = find(b);

(2)维护size

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

// 返回x的祖宗节点
int find(int x){	
    //每个节点直接与其Find()操作最终得到的节点连接，路径压缩
    if (p[x] != x) 
        p[x] = find(p[x]);//递归查询
    return p[x];
}

// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ ){
    p[i] = i;
    size[i] = 1;
}

// 合并a和b所在的两个集合：
size[find(b)] += size[find(a)];
p[find(a)] = find(b);

(3)带权

先记录下原本父节点的编号，因为在路径压缩后父节点就变为根节点了。将当前节点的权值加上原本父节点的权值，父节点的权值为父节点到根节点的权值，因此加上这个权值就会得到当前节点到根节点的权值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//查找
int find(int x){
	if (x != p[x]){
		int t = p[x];
		p[x] = find(p[x]);
		value[x] += value[t];//当前节点到根节点的权值。 
	}
	return p[x];
}

//合并
int px = find(x);
int py = find(y);
if (px != py){
    p[px] = py;
    value[px] = -value[x] + value[y] + s;//闭环
}

img

Kruskal

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// N 要为 点数的平方

int n, m;       // n是点数，m是边数
int p[N];       // 并查集的父节点数组

struct Edge{     // 存储边
    int a, b, w;

    bool operator< (const Edge &W)const{
        return w < W.w;
    }
}edges[M];

int find(int x){     // 并查集核心操作
    if (p[x] != x) 
        p[x] = find(p[x]);
    return p[x];
}

//m条边
int kruskal(){
    sort(edges, edges + m);

    for (int i = 1; i <= n; i ++ ) 
        p[i] = i;    // 初始化并查集

    int res = 0, cnt = 0;
    for (int i = 0; i < m; i ++ ){
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b);
        if (a != b)     // 如果两个连通块不连通，则将这两个连通块合并
        {
            p[a] = b;
            res += w;
            cnt ++ ;
        }
    }

    if (cnt < n - 1) return INF;
    return res;
}

双指针

对于一个序列，用两个指针维护一段区间

1
2
3
4
5
6
7
8
for (int i = 0, j = 0; i < n; i ++){
    while (j < i && check(i, j)) j ++ ;

```
// 具体问题的逻辑
```

}

扩展欧几里得

1
2
3
4
5
6
7
8
9
10
// 求x, y，使得ax + by = gcd(a, b)
int exgcd(int a, int b, int &x, int &y){
    if (!b){
        x = 1; y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= (a/b) * x;
    return d;
}

组合数

加法原理

a位巨佬中抽出b位巨佬的方案数 可以 分为两类

1.选抽风巨佬 只要从a-1位巨佬中选出b-1位巨佬
2.不选抽风巨佬 从剩下a-1位巨佬中选出b位巨佬

1
2
3
4
5
6
7
// c[a][b] 表示从a个苹物品中选b个的方案数
for (int i = 0; i < N; i ++ )
    for (int j = 0; j <= i; j ++ )
        if (!j) 
            c[i][j] = 1; //边界初始化
        else 
            c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;

递归实现组合数枚举

参数：临时数组的下标、起始下标、[已经选的数字个数…]（int u , int start, […]）

**变式：**1.要求每个数字可以重复选取，改为 dfs( u + 1, i )

​ 2.去重问题：给定的集合中有多个重复元素，要求在满足题意的子集中，不能有完全相同的子集。翻译：不能用同一层使用过的元

​ 素。需要先排序并引入bool数组。更具体的，如下代码所示。

​ 3.未必是在n个数中选m个固定的数， 可以在一定的条件下保存答案并退出

​ 4.排列问题需要用到used数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void f(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {
    if (sum == target) {
        result.push_back(path);
        return 0；
    }
    
    //一点剪枝  
    for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
        // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
        // used[i - 1] == false，说明同一树层candidates[i - 1]使用过   已经回到了上一层    
        // 要对同一树层使用过的元素进行跳过
        if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
            continue;
        }
        sum += candidates[i];
        path.push_back(candidates[i]);
        used[i] = true;
        backtracking(candidates, target, sum, i + 1, used); 
        used[i] = false;
        sum -= candidates[i];
        path.pop_back();
    }
}

//在dfs前 先排好序 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
using namespace std;

int n, m; //n 个数 选 m 个
const int N = 20;
int a[20];

void dfs(int u, int start){

    if(u == m + 1){
        for (int i = 1; i <= m; i ++ )
            cout << a[i] << ' ';
        cout << endl;
        return ;
    }

    for (int i = start; i <= n; i ++ ){
        a[u] = i;
        dfs(u + 1, i + 1);
        a[u] = 0;
    }
}

int main(){

    cin >> n >>  m;

    dfs(1, 1); //个数 / 当前起始位置

    return 0;
}

二进制枚举

在集合中选出所有子集 时间复杂度为2^n

1
2
3
4
5
6
7
8
9
10
// 二进制枚举所有情况
for ( int i = 0; i < 1 << n; i++){
    // i 从 1 ~ 1 << n, 如果二进制表示为1则代表选这一位，为0则不选
    // 需要输出最小字典序,用来与res比较
    for (int j = 0; j < n; j ++){
        // cout << i << " " << j << " " << (i >> j & 1 ) << endl;
        if( i >> j & 1 ) // 第j位是1
        {  }
 }
}

DP

要点：1.初始化 2.dp的严格定义 3.不重不漏地转移 4.套经典模型

走方格

一个人位于一个 m x n 网格的左上角，每次只能向下或者向右移动一步。网格中有障碍物。那么从左上角到右下角会有多少条不同的路径？

1
2
3
4
5
6
7
8
9
10
11
12
//初始化  从(0, 0)的位置到(i, 0)的路径只有一条，所以dp[i][0]一定为1，dp[0][j]同理。
for (int i = 0; i < m; i++)  dp[i][0] = 1;
for (int j = 0; j < n; j++)  dp[0][j] = 1;
		
for (int i = 1; i < m; i++) {
    for (int j = 1; j < n; j++) {
        if (有障碍) 
			continue;
        dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
    }
}
cout << dp[m - 1][n - 1] << endl;

爬楼梯

一步一个台阶，两个台阶，三个台阶，直到 m个台阶，有多少种方法爬到n阶楼顶。 计数问题。

1
2
3
4
5
6
7
8
9
10
11
int climbStairs(int n) {
    vector<int> dp(n + 1, 0);
    dp[0] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) { // 把m换成2，就可以AC爬楼梯这道题
        	if (i - j >= 0) 
        		dp[i] += dp[i - j];
        }
    }
    return dp[n];
}

背包

外层物品正序，内层背包倒序或者正序。

01背包

有一维和二维表示

1
2
3
4
5
6
7
8
// 初始化
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
    	dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);  //放或者不放
    }
}
cout << dp[bagWeight] << endl;

完全背包

完全背包的物品是可以添加多次的，所以要从小到大去遍历

1
2
3
4
5
6
// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

线性

最长上升子序列

根据数据范围选择不同的处理方式

1
2
3
4
5
6
7
8
9
10
11
12
for(int i = 0; i < n; i++)
	cin >> a[i];
	
//注意边界
for(int i = 0; i < n; i++){
    f[i] = 1;
    for(int j = 0; j < i; j++)
        if(a[i] > a[j])
            f[i] = max(f[i], f[j] + 1);
    
    res = max(res, f[i]);
}	
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
//优化  贪心 二分 将原有序列中 大于或等于当前数字的数 替换为 当前数
//数组q维护一段长序列 长度为len 
int len = 0;
for(int i = 0; i < n; i++){
    int l = 0, r = len;
    while(l < r){
        int mid = (l + r + 1) >> 1;
        //模板二  找出最靠近数字的下标   替换掉他之后的那个数 
        if(q[mid] < a[i])
        	l = mid;
        else
        	r = mid - 1;
    }
    len = max(len, r + 1);
    q[r + 1] = a[i];
    
    f[i] = r + 1;  //记录长度 
}

cout << len << endl;
//7
//3 1 2 1 8 5 6

//输出路径
for(int i = k - 1, t = len; i > 0; i--){
    if(f[i] == t){
        res[t] = cnt[i];
        t--;
    }
    if(t == 0)
        break; 
}

for(int i = 1; i <= len; i++)
    cout << res[i] << ' ';

变式：最大子序列和。 f[i] = max(f[i], f[j] + a[i]);

最长公共子序列

1
2
3
4
5
6
7
8
9
10
11
vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
for (int i = 1; i <= text1.size(); i++) {
    for (int j = 1; j <= text2.size(); j++) {
        if (text1[i - 1] == text2[j - 1]) {
        	dp[i][j] = dp[i - 1][j - 1] + 1;
        } else {
        	dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
        }
    }
}
return dp[text1.size()][text2.size()];

变式1：给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

思路：只要求出两个字符串的最长公共子序列长度即可，那么除了最长公共子序列之外的字符都是必须删除的，最后用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数。

变式2：给定字符串 s 和 t ，判断 s 是否为 t 的子序列。 例如，"ace"是"abcde"的一个子序列，而"aec"不是 。

1
2
if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i][j - 1];

最大连续子序列和

1
2
3
4
5
6
7
8
dp[0] = nums[0];
int result = dp[0];
for (int i = 1; i < nums.size(); i++) {
    dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式
    if (dp[i] > result) 
    	result = dp[i]; // result 保存dp[i]的最大值
}
return result;

连续子数组的最大和

1
2
3
4
5
6
7
int res = -0x3f3f3f3f, sum = 0;
for (int i = 0; i < n; i++){
    sum = max(sum, 0) + nums[i];
    res = max(res, sum);
 }

return res;

变式: 二维数组的最大子矩阵

编辑距离

初始化的坑。

dp[i]：word2为空字符串，以i-1为结尾的字符串word1要删除多少个元素，才能和word2相同呢，很明显dp[i] = i。

dp[j]的话同理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
for (int i = 1; i <= word1.size(); i++) {
    for (int j = 1; j <= word2.size(); j++) {
        if (word1[i - 1] == word2[j - 1]) {
            dp[i][j] = dp[i - 1][j - 1];
        }
        else {
            //添加 删除   替换
            dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
        }
    }
}
return dp[word1.size()][word2.size()];

变式：只能有删除操作，求最小步数。

  • 当word1[i - 1] 与 word2[j - 1]相同的时候 dp[i] = dp[i-1] ;
  • 当word1[i - 1] 与 word2[j - 1]不相同的时候，有三种情况：

情况一：删word1[i - 1]，最少操作次数为dp[i-1] + 1

情况二：删word2[j - 1]，最少操作次数为dp[i+1]

情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i-1]+2

那最后当然是取最小值

1
dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});

区间

最长回文子序列

  • 如果s[i] == s[j] 构造出以s[i]为开头和s[j]为结尾的回文子序列
  • 如果s[i] != s[j] 不可能构造以s[i]开头同时以s[j]结尾的最长回文子序列
1
2
3
4
5
6
7
8
9
10
11
12
for(int i = 0; i < n; i ++ ) 
    dp[i][i] = 1;//长度为1的回文子序列 初始化

for(int len = 2; len <= n; len ++ )//枚举长度
    for(int i = 0; i + len - 1 < n; i ++ ){//枚举起点
        int l = i, r = i + len - 1; //区间左右端点
        if(s[l] == s[r]) 
            dp[l][r] = dp[l + 1][r - 1] + 2;
        else 
            dp[l][r] = max(dp[l][r - 1], dp[l + 1][r]);
    }
return dp[0][n - 1];

合并石子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
for (int i = 1; i <= n; i ++) {
	cin >> a[i];
	s[i] += s[i - 1] + a[i];//前缀和
}

memset(f, 0x3f, sizeof f);

// 区间 DP 枚举套路：长度+左端点 
for (int len = 1; len <= n; len ++) { // len表示[i, j]的元素个数
    for (int i = 1; i + len - 1 <= n; i ++) {
        int j = i + len - 1; // 自动得到右端点
        if (len == 1) {
            f[i][j] = 0;  // 边界初始化  dp初始化
            continue;
        }

        for (int k = i; k < j; k ++) { // 必须满足k + 1 <= j
            f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);
        }
    }
}
cout << f[1][n] << endl;

计数(背包恰好装满)

01背包和完全背包变式，只有求排列数时才要改变循环顺序。如果求组合数就是外层for循环遍历物品，内层for遍历背包。如果求排列数就是外层for遍历背包，内层for循环遍历物品。

首先判断是01背包还是完全背包，即确定了遍历背包是正序还是倒序。然后默写

求组合类问题：

1
2
3
dp[0] = 1;

dp[j] += dp[j - nums[i]];

求排列类问题：遍历外背包内物品

1
2
3
4
5
6
7
8
9
dp[0] = 1;

for(int i = 0; i <= target; i++){
    for(int j = 0; j < nums.size(); j++){
        if(i >= nums[j]) 
            dp[i] += dp[i - nums[j]];
    }
}
return dp[target];

树形

eg. 求最大的子树。f[u] 在以u为根的子树中 所有联通块的权值的最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <iostream>
#include <cmath>
#include <algorithm>
#define INF 1e8
using namespace std;
const int N = 2e5 + 1e2;

int cnt, a, b, n;
int res = -INF;
int h[N], f[N], w[N];

//比常规的加边 少了一个边权  在本题中权重以点权的形式表现出来
struct edge{
	int to;
	int next;
} e[N];// 邻接表存储所有边

void add(int u, int v) {
	cnt++;
	e[cnt].to = v;
	e[cnt].next = h[u];//注意顺序
	h[u] = cnt;        //注意顺序
}

void dfs(int u, int father){
	
    f[u] = w[u];

    for(int i = h[u]; i; i = e[i].next) {

        int j = e[i].to;
        //cout << j << endl;
        if(j == father)
            continue;

        //在这里做处理时    用父节点信息更新子节点
        
        dfs(j, u);  //子 / 父 

        if(f[j] > 0) {
            f[u] += f[j];
            //cout << f[u] << endl;
        } 
        //自底向上 用子节点更新父节点信息
	}
} 

int main(){
	cin >> n;
    for(int i = 1; i <= n; i ++) 
        cin >> w[i]; //边权 

    int m = n - 1;
    while(m--){

        cin >> a >> b;
        add(a, b);
        add(b, a);
    }

    dfs(1, -1); //子 / 父 

    for(int i = 1; i <= n; i ++) {
        res = max(res, f[i]);
        //cout << f[i] << endl;
    }

    cout << res << endl;

    return 0;
}

状态机

多维dp 不同维度存储不同信息

数位

windy数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

const int N = 20;
int f[N][N], l, r;
//长度  最后一位的数字 

void init(){

    //只有一位时   
    for(int i = 0; i <= 9; i++)
        f[1][i] = 1;

    for(int i = 2; i <= N; i++) 
        for(int j = 0; j <= 9; j++)
            for(int k = 0; k <= 9; k++)
                if(abs(j - k) >= 2)
                //固定好外层的那一位 
                    f[i][j] += f[i - 1][k];	
}

int dp(int n){
    vector <int> a;

    //注意last初始 
    int res = 0, last = -1;

    if(!n) return 0;

    while(n){
        a.emplace_back(n % 10);
        n /= 10;
    }

    int len = a.size() - 1;

    //没有前导 0 
    for(int i = len; i >= 0; i--){
        int x = a[i];

        //左分支 
        //枚举 该位上可以出现的数字
        if(i == len){
            for(int j = 1; j < x; j++)
                if(abs(j - last) >= 2)
                    res += f[i + 1][j];
        }else{
            for(int j = 0; j < x; j++)
                if(abs(j - last) >= 2)
                    res += f[i + 1][j];
        }

        //右分支 
        if(abs(x - last) < 2)
            break;
        else 
            last = x;

        if(!i)
            res++; 
    } 

    //答案小于a.size()位的
    for(int i = 1; i <= len; i++)
        for(int j = 1; j <= 9; j++)
            res += f[i][j];

    return res; 
} 

int main(){
	init(); 

    cin >> l >> r;

    cout << dp(r)- dp(l - 1) << endl;

    return 0;
}

状态压缩

最短Hamilton路径。给定一张 n 个点的带权无向图，点从 0~n−1 标号，求起点 0 到终点 n−1 的最短路径。不重不漏地经过每个点恰好一次。

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//w矩阵保存各点之间的距离
memset(f, 0x3f, sizeof f);              // 初始化为无穷大
f[1][0] = 0;    // 表示只有起点0且最后位于起点0的路线的长度是0，此时点集i的最后一位是1，其余为0，因为点集只有起点0，故i=1

for (int i = 0; i < 1 << n; i ++ )          // 穷举所有可能的点集
    for (int j = 0; j < n; j ++ )           // 从当前点集找一个点（二进制串中位为1的位置）
        if (i >> j & 1)
            for (int k = 0; k < n; k ++ )    // 从当前点集找另外一个点（可以和之前找的相同）
                if (i >> k & 1)
                    f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);   // 尝试从后找的点到达点j

//起始点固定
// 0 -> k -> j
// 第一个下标状态集合

**分割等和子集：**将数组分割成两个子集，使得两个子集的元素和相等。 01背包

1
2
3
4
5
6
7
8
9
10
11
12
13
//价值为数字本身

int target = sum / 2;

// 开始 01背包
for(int i = 0; i < nums.size(); i++) {
    for(int j = target; j >= nums[i]; j--) { 
    	dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
    }
}
// 集合中的元素正好可以凑成总和target
if (dp[target] == target) 
	return true;

**粉碎石子：**有一堆石头， 每一回合，从中选出任意两块石头，然后将它们一起粉碎。 最后，最多只会剩下一块石头。返回此石头最小的可能重量。

尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，这样就化解成01背包问题了。 与上题类似，改return即可。

1
return sum - dp[target] - dp[target];

**目标和：**给定一个数组和一个目标数。对于数组中的任意一个整数，从 + 或 -中选择一个符号添加在前面。返回可以使最终数组和为目标数 S的所有添加符号的方法数。

转化为01背包问题。假设加法的总和为x，那么减法对应的总和就是sum - x。

所以我们要求的是 x - (sum - x) = S 即x = (S + sum) / 2。此时问题就转化为，装满容量为x背包，有几种方法。组合计数问题。

1
dp[j] += dp[j - nums[i]];

**零钱兑换：**给定不同面额的硬币和一个总金额。计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。 同上，计数完全背包问题。装满容量为总金额的背包。

**零钱兑换变式：**求凑成总金额所需的最少的硬币个数。

1
dp[j] = min(dp[j - coins[i]] + 1, dp[j]);

**组合总和：**给定一个由正整数组成且不存在重复数字的数组，找出和为给定目标正整数的组合的个数。 同上，计数完全背包问题。装满容量为目标正整数的背包。

**完全平方数：**找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。需要让组成和的完全平方数的个数最少。给你一个整数 n ，返回和为 n 的完全平方数的 最少数量 。

1
2
3
4
5
6
7
8
9
//背包的下限是要大于完全平方数的
vector<int> dp(n + 1, INT_MAX); 
dp[0] = 0;
for (int i = 1; i <= n; i++) { // 遍历物品
    for (int j = i * i; j <= n; j++) { // 遍历背包
        dp[j] = min(dp[j - i * i] + 1, dp[j]);
    }
}
return dp[n];